In the grid below, box A shares walls or corners with 3 other boxes, B, E, and F. Determine how many walls or corners each of the other boxes share.
Solution
What would the numbers be in a 5 x 5 grid?
Problem of the Month - April 2026
Pick any 3 numbers from the following list, circle them, and find their sum
1 , 1 , 1 , 4 ,4 , 4, 7 , 7 , 7, 10, 10 ,10
Repeat the process with a new set of numbers from the original list.
What do you notice about the sums?
Can you explain why this happens?
Answer:
The sum is always a multiple of 3.
Problem of the Month - May 2026
Each number from 1 to 6 replaces one of the letters P, Q, R, S, T, and U.
The sum of P and Q is 5 and the difference between R and S is 5.
If T is greater than U, what number replaces the letter T?
Source: 2023 Gauss Math Contest
Problem of the Month - March 2026
Five different numbers in a list have a median of 10 and a range of 7.
What is the smallest possible number in the list?
Source: 2024 Gauss Math Contest
Problem of the Month - February 2026
Imagine two red frogs and two blue frogs sitting on lily pads, with an empty lily pad in between them.
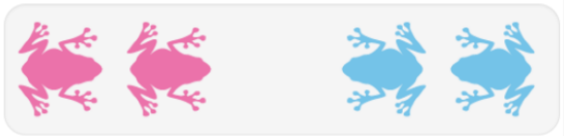
Frogs can slide onto an empty lily pad that is beside them or jump over a frog onto an empty lily pad.
Frogs can't jump over more than one frog.
Frogs can jump forward or backwards
Problem of the Month - January 2026
A standing desk has 31 height settings, numbered from the lowest height, 1, to the highest height, 31. Since the desk is not working properly, when the up button is pressed, the desk goes up 6 settings at a time if possible, otherwise it does not move. When the down button is pressed, the desk goes down 4 settings at a time if possible; otherwise, it does not move. If the desk starts at setting number 1 , how many of the 31 settings will the desk be able to stop at?
Source: 2024 Gauss Math Contest