Problem of the Month - April 2026
Pick any 3 numbers from the following list, circle them, and find their sum
1 , 1 , 1 , 4 ,4 , 4, 7 , 7 , 7, 10, 10 ,10
Repeat the process with a new set of numbers from the original list.
What do you notice about the sums?
Can you explain why this happens?
Problem of the Month - March 2026
Five different numbers in a list have a median of 10 and a range of 7.
What is the smallest possible number in the list?
Source: 2024 Gauss Math Contest
Problem of the Month - February 2026
Imagine two red frogs and two blue frogs sitting on lily pads, with an empty lily pad in between them.
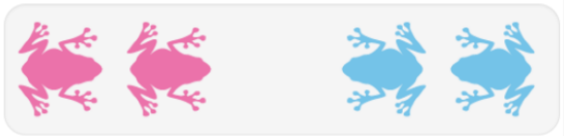
Frogs can slide onto an empty lily pad that is beside them or jump over a frog onto an empty lily pad.
Frogs can't jump over more than one frog.
Frogs can jump forward or backwards
Problem of the Month - January 2026
A standing desk has 31 height settings, numbered from the lowest height, 1, to the highest height, 31. Since the desk is not working properly, when the up button is pressed, the desk goes up 6 settings at a time if possible, otherwise it does not move. When the down button is pressed, the desk goes down 4 settings at a time if possible; otherwise, it does not move. If the desk starts at setting number 1 , how many of the 31 settings will the desk be able to stop at?
Source: 2024 Gauss Math Contest
November - Problem of the Month
The number 29 is interesting because when the sum of the digits (2+9) is added to the product of the digits (2x9) the answer is 29, the number that we started out with (11+18=29).
Can you find another number with these properties?
Solution:
59
5 + 9 = 14
5 × 9= 45
14 + 45 = 59
What do you notice about these numbers?
Could it work with a 3-digit number?
Problem of the Month - September 2026
Sums of the Unexpected
The number 15 can be written as the sum of consecutive whole numbers in three ways.
15 = 7 + 8
15= 4 + 5 + 6
15= 1 + 2 + 3 + 4 +5
In how many ways can you write 105 as the sum of consecutive whole numbers?
In how many ways can you write 24 as the sum of consecutive whole numbers?
(A consecutive whole number is a number that comes directly after another whole number in a sequence, e.g. 5,6,7,8,9…)
Problem of the Month - June 2025
You will need two six-sided dice to play this game. Roll both dice and create a two digit number by taking the larger number followed by the smaller number. If the numbers are the same, then the two digit number is going to be either 11, 22, 33, 44, 55, or 66 depending on what you rolled. You win if you get a two digit number less than 50. Play the game 100 times to determine your experimental probability of winning.
Problem of the Month - May
A bag contains 5 blue blocks, 7 green blocks, and 6 red blocks. Blocks are selected randomly, one at a time, from the bag. What is the minimum number of blocks that need to be removed from the bag to be certain that there are three that are the same colour?
Solution
Problem of the Month - April 2025
You have a 7 minute and a 4 minute hourglass timer. How would you use these to measure 9 minutes?
Solution
Flip the 7 minute and 4 minute timer at the same time. When the 4 is done, flip it again. When the 7 minute timer is done, flip it again. When the 4 minute is done, flip the 7 minute timer. When the 7 minute timer is done, 9 minutes will have passed from the first time the timers were flipped.
Problem of the Month - March 2025
You roll a fair six sided die twice. Your score is whichever roll was higher. For example, if you rolled a 4 and then a 3, your score would be 4. What is the probability that your score will be 5?
Solution: If you roll a six sided die twice, there are 36 possible outcomes. The ones that would result in a score of 5 are:
1,5
2,5,
3,5
4,5
5,5
5,4
5,3
5,2
5,1